Classes | |
| struct | mtcore::math::GCD< A, B > |
| Template to get GCD of numbers. More... | |
| struct | mtcore::math::LCM< A, B > |
| Template to get LCM of numbers. More... | |
| struct | mtcore::math::MultRatios< T1, T2 > |
| Template to multiply two std::ratio numbers. More... | |
| struct | mtcore::math::AddRatios< T1, T2 > |
| Template to add two std::ratio numbers. More... | |
| struct | mtcore::math::RatioParts< T > |
| Template to get the Numerator and Denominator of a std::ratio. More... | |
| struct | mtcore::math::InvertRatio< T > |
| Template to invert a ratio number. More... | |
| struct | mtcore::math::NegateRatio< T > |
| Template to negate the power of a ratio. More... | |
| struct | mtcore::math::IntPowRatioImpl< T, Pow, Odd, Neg, Z > |
| Template to get the integer power (positive or negative) of a ratio. More... | |
Functions | |
| template<typename T, typename R = double> | |
| constexpr R | mtcore::math::floor_constexpr (T num) noexcept |
| Constexpr floor function. | |
| template<typename T, typename R = double> | |
| constexpr R | mtcore::math::ceil_constexpr (T num) noexcept |
| Constexpr ceil function. | |
| template<typename T, typename R = T> | |
| constexpr R | mtcore::math::floor (T num) noexcept |
| Floors a number with support for constexpr and fast runtime compilation. | |
| template<typename T, typename R = T> | |
| constexpr R | mtcore::math::ceil (T v) noexcept |
| Ceils a number with support for constexpr and fast runtime compilation. | |
| template<typename L, typename R, typename Res = L> | |
| constexpr Res | mtcore::math::mod (L left, R right) noexcept |
| Calculates the mathematical mod of two numbers. | |
| template<typename T> | |
| constexpr auto | mtcore::math::mod_range (T x, i64 a, i64 b) noexcept -> T |
| x mod [a..b) | |
| template<typename L, typename R, typename Res = L> | |
| constexpr auto | mtcore::math::amod (L x, R y) noexcept -> Res |
| x mod [1..y] | |
| template<typename T, typename R = T> | |
| constexpr auto | mtcore::math::approx_eq (T x, R y, T epsilon=T{0.000001}) noexcept -> bool |
| Checks if two numbers are approximately equal (within epsilon distance) | |
| template<typename T> | |
| constexpr int | mtcore::math::sign (const T &v) |
| Gets the sign (1 for positive, -1 for negative, 0 for zero) | |
| template<typename L> | |
| constexpr L | mtcore::math::abs (L l) |
| Gets absolute value of a number. | |
| template<typename T> | |
| constexpr T | mtcore::math::int_pow (T val, int exp) |
| Raises to an integer power (positive or negative) | |
| template<std::integral T> | |
| constexpr T | mtcore::math::gcd (T a, T b) |
| Calculates the GCD (Greatest Common Divisor) of two integer numbers. | |
| template<std::integral T> | |
| constexpr T | mtcore::math::lcm (T a, T b) |
| Calculates the LCM (Least Common Multiple) of two integer numbers. | |
Detailed Description
Function Documentation
◆ abs()
|
constexpr |
Gets absolute value of a number.
- Template Parameters
-
L Type to get absolute value of
- Parameters
-
l Value to get absolute of
Definition at line 188 of file core/mtcore/math/core.hpp.


◆ amod()
|
constexprnoexcept |
x mod [1..y]
Definition at line 151 of file core/mtcore/math/core.hpp.


◆ approx_eq()
|
constexprnoexcept |
Checks if two numbers are approximately equal (within epsilon distance)
Definition at line 161 of file core/mtcore/math/core.hpp.
◆ ceil()
|
constexprnoexcept |
Ceils a number with support for constexpr and fast runtime compilation.
Also accepts ints, though ints are a noop.
- Template Parameters
-
T Type to floor R Type to cast result to (default is no cast)
- Parameters
-
v Number to floor
Definition at line 103 of file core/mtcore/math/core.hpp.

◆ ceil_constexpr()
|
constexprnoexcept |
Constexpr ceil function.
Prefer math::ceil for better runtime support.
- See also
- mtcore::math::ceil
- Template Parameters
-
T R
- Parameters
-
num
Definition at line 62 of file core/mtcore/math/core.hpp.

◆ floor()
|
constexprnoexcept |
Floors a number with support for constexpr and fast runtime compilation.
Also accepts ints, though ints are a noop.
- Template Parameters
-
T Type to floor R Type to cast result to (default is no cast)
- Parameters
-
num Number to floor
Definition at line 82 of file core/mtcore/math/core.hpp.

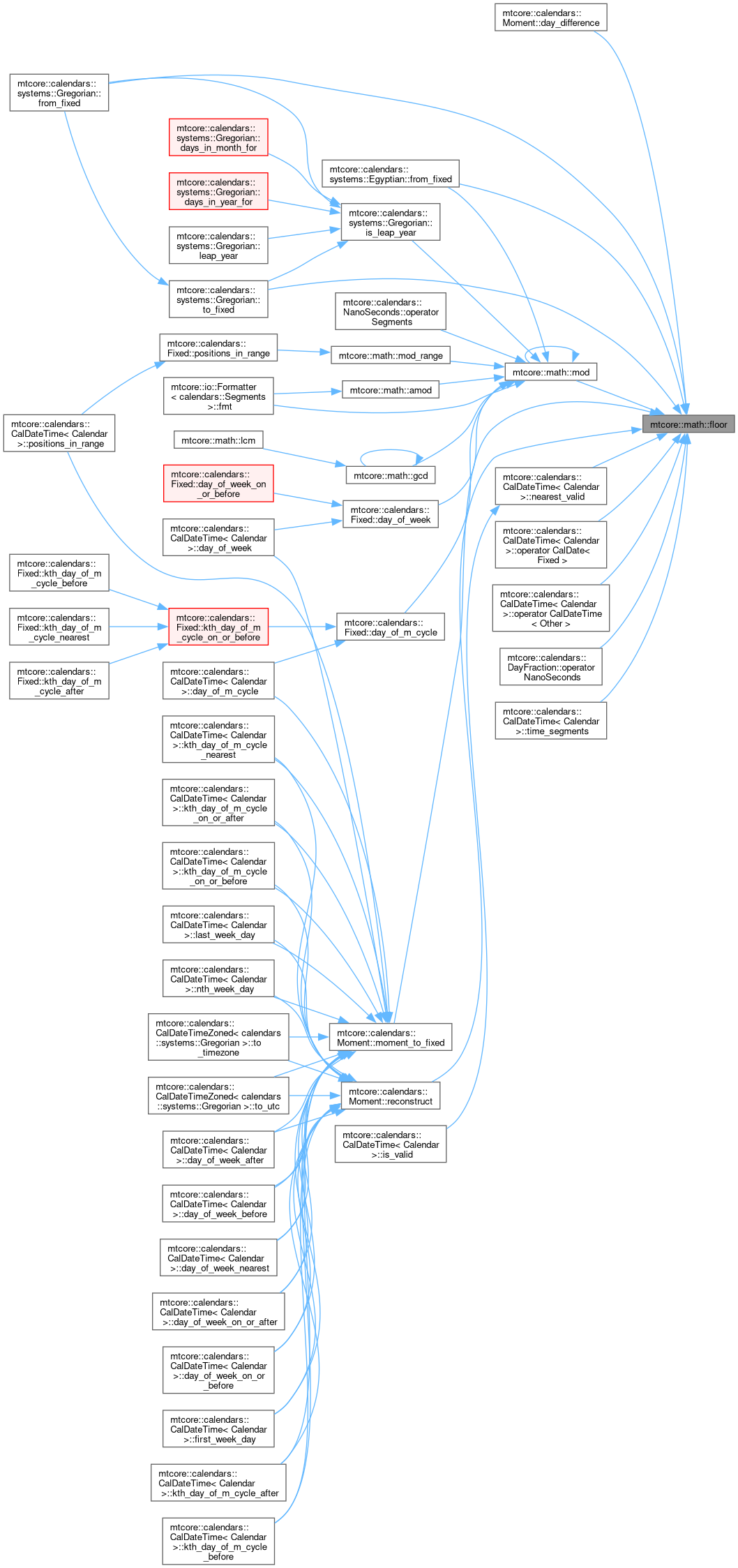
◆ floor_constexpr()
|
constexprnoexcept |
Constexpr floor function.
Prefer math::floor for better runtime support.
- See also
- mtcore::math::floor
- Template Parameters
-
T R
- Parameters
-
num
Definition at line 41 of file core/mtcore/math/core.hpp.
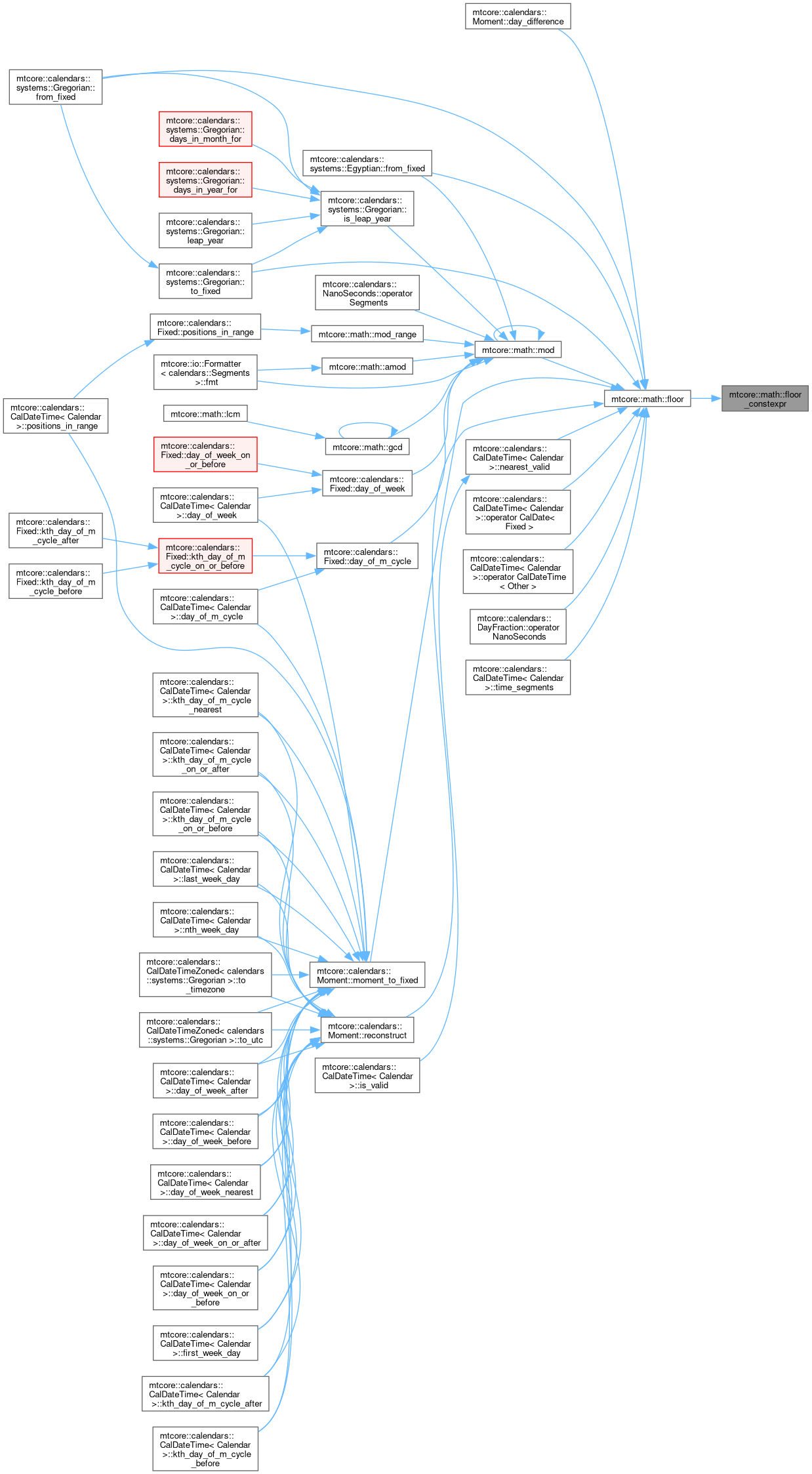
◆ gcd()
|
constexpr |
Calculates the GCD (Greatest Common Divisor) of two integer numbers.
- Template Parameters
-
T Type of values to operate on
- Parameters
-
a value 1 b value 2
Definition at line 223 of file core/mtcore/math/core.hpp.


◆ int_pow()
|
constexpr |
Raises to an integer power (positive or negative)
- Template Parameters
-
T Type of value to exponentiate
- Parameters
-
val Value to exponentiate exp Exponent to raise to
Definition at line 200 of file core/mtcore/math/core.hpp.


◆ lcm()
|
constexpr |
Calculates the LCM (Least Common Multiple) of two integer numbers.
- Template Parameters
-
T Type of values to operate on
- Parameters
-
a value 1 b value 2
Definition at line 238 of file core/mtcore/math/core.hpp.

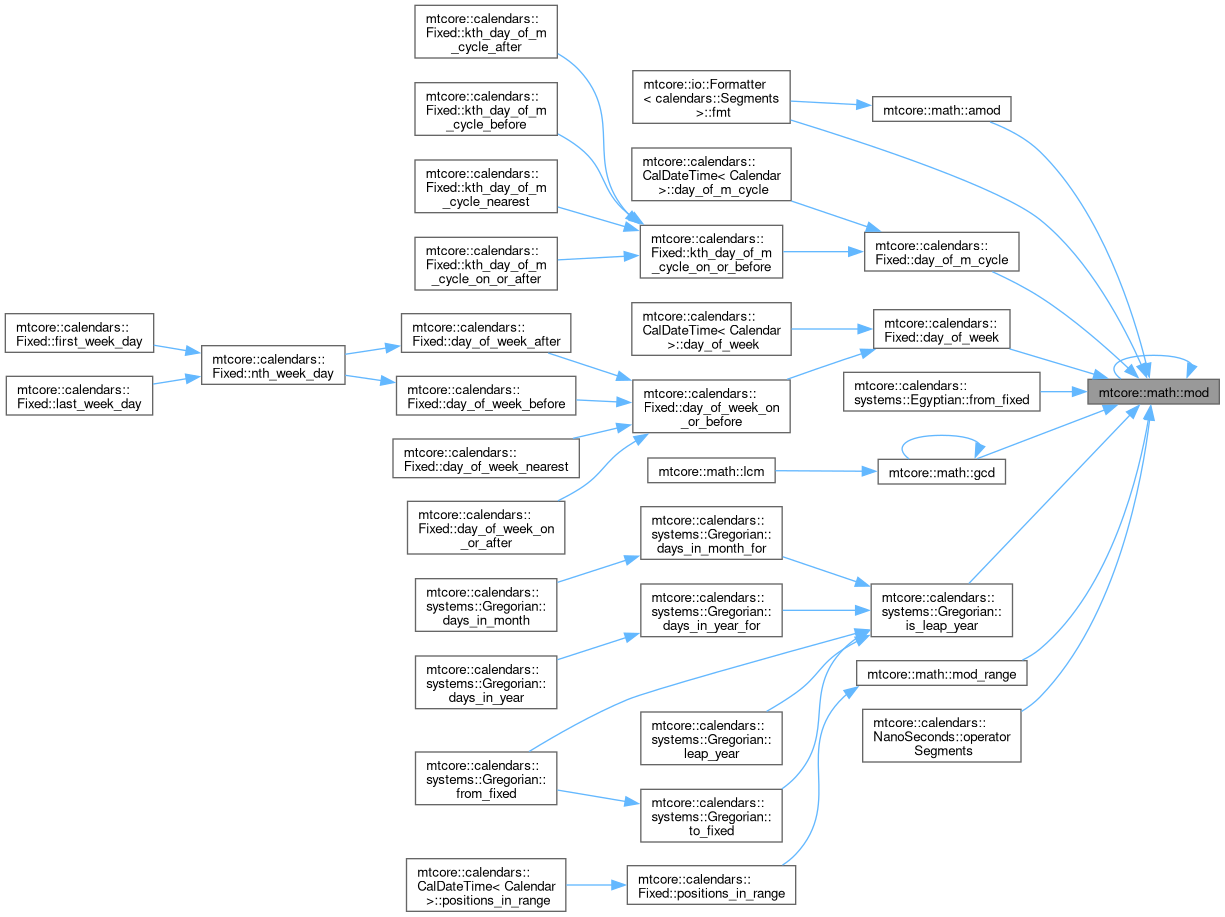
◆ mod()
|
constexprnoexcept |
Calculates the mathematical mod of two numbers.
Has different negative number handling than % which allows it to be better for indexes. Also, it's more consistent across platforms and handles floating point numbers as well.
- Template Parameters
-
L Type of left operand R Type of right operand Res Type of result
- Parameters
-
left Left operand right Right operand
- Returns
- Mod
Definition at line 128 of file core/mtcore/math/core.hpp.

◆ mod_range()
x mod [a..b)
Definition at line 142 of file core/mtcore/math/core.hpp.


◆ sign()
|
constexpr |
Gets the sign (1 for positive, -1 for negative, 0 for zero)
Definition at line 171 of file core/mtcore/math/core.hpp.
